When you run a program, do you ever wonder why it's taking so long to run? Or perhaps you see your current program takes up half of the RAM on your computer? The problem might have to deal with Algorithm Complexity.

What is an Algorithm?

To start, an algorithm is a step-by-step approach of precise instruction to solve a specific problem. It is important to note that it is independent of any programming language. You can represent algorithms by using pseudocode, flow chart, structured chart, etc.

Let's start with an example. Let's say that you want to create an algorithm that helps adds up the sum of two numbers. I will be using a flow chart and pseudocode to demonstrate.

flow chart:

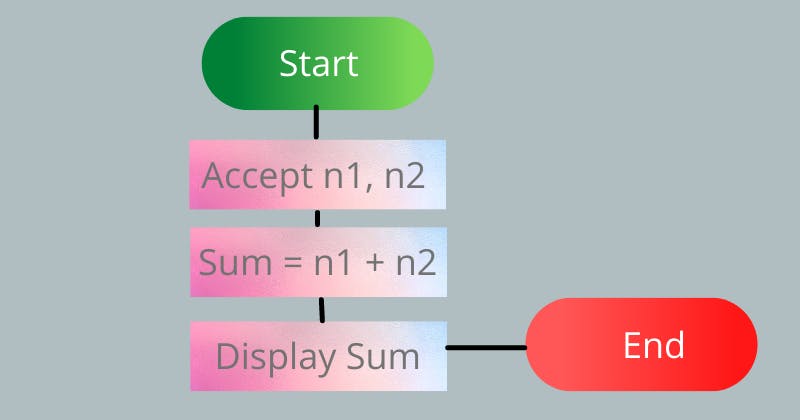
pseudocode:

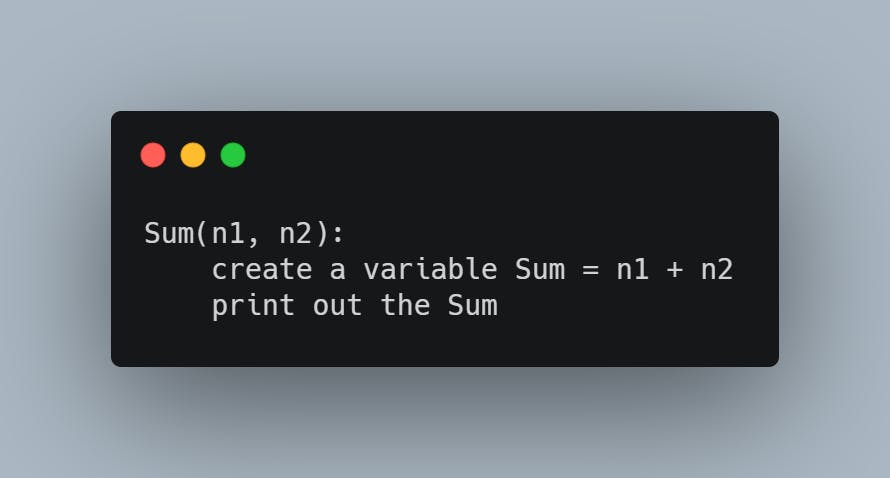
Being able to solve the problem before jumping into programming helps with logical errors. A logical error is when you don't get the desired result from your program. An example of this is if I were to add 2 + 2 and expect 4, but instead, I got 6. When you write your algorithm, it will be easier to find where it went wrong. It's not a common skill most self-learned programmer have. But it's a skill that I recommend programmers learn.

What is Algorithm Complexity?

Algorithm Complexity is the measure of time and space requirement of an execution of code.Let's us look at an example of three different algorithm that solves the same problem. The problem being to display the sum of positive integers up to n.

The First Algorithm

Explanation

We see here it is the simplest solution to get the end result that we want. The algorithms is using a for loop to iterate from 1 to n. The idea of the algorithm is:

1 + 2 + 3 + 4 + 5 + ... + n

The Second Algorithm

Explanation

It is the same solution just like the first algorithm but instead there are two for loops in the algorithm. The idea of the algorithm is the summation of n

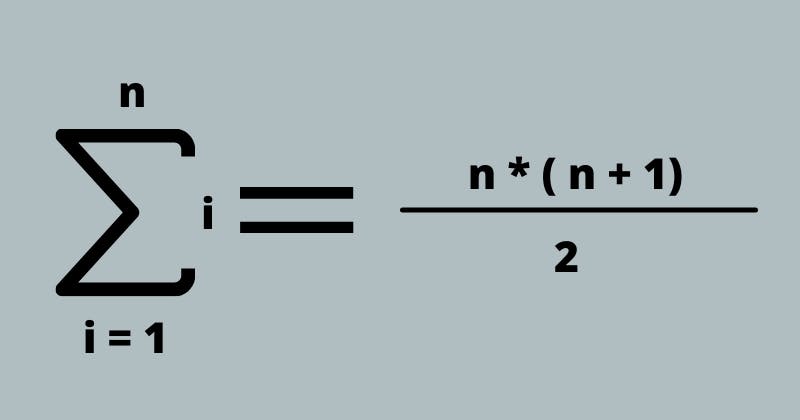
The Third Algorithm

Explanation

It's like the other two and instead uses the summation to calculate the sum of n. Algorithm 3 is the fastest of the three algorithm

So, how would you choose which of the three algorithms to solve the problem of displaying the sum of positive integers up to n?

That depends on what you are looking for in a given algorithm. Which of the three criteria is important to you? Is it the speed, simplicity, or efficiency algorithm? When talking about the efficiency of an algorithm, it's important to choose the most efficient one.

Measuring Algorithm Complexity

Measuring the efficiency of an algorithm can be broken down into two categories: Time and Space complexity.

• Time complexity focuses on the time needed to execute the program from the given algorithm.

Example: When you are waiting at a restaurant for your food and let's say the food comes out in an hour because of a poor design in management in the kitchen, you might be furious. Compared to when you get it in ten minutes because of good management in the kitchen.

• Space complexity focuses on how much memory the algorithm uses up when the program runs.

Example: Let's say you are putting away clothes, and you shove all of them into the closet without organizing them. Yes, it might take less time now to put away your clothes. However, you are going to spend more time looking for particular clothes and have less closet space. Compared to when you take the time to organize your clothes. The process might take longer. But in the end, you have more space in your closet.

In the end, you will usually choose time or space complexity to help make a good algorithm. In the next article in the series, I will be taking a deeper dive into how time complexity works in something called the Big O notation.

If you want more information on the resources I used when I took data structure in university here is the link .

I hope this helps give you a basic idea of how algorithm complexity works! See you on the next article.